Часто буває так, що, розв`язуючи задачі, дуже далекі одна від одної за змістом, ми приходимо до однієї і тієї самої математичної моделі.

Особливість математики як науки
полягає в тому, що вона розробляє
способи оперування з тією чи
іншою математичною моделлю,
яку потім використовують
спеціалісти з інших галузей знань.
Сьогодні йтиметься про
принципово нову для вас
математичну модель. Отже,
розгляньмо дві різні задачі: фізичного і геометричного змісту, в процесі
розв`язування яких саме і виникає нова математична модель.
Нехай деяке тіло (матеріальна
точка) рухається по прямій, на
якій задані початок відліку,
одиниця виміру(метр) і напрям.
Закон руху задано формулою
S=s(t), де t – час (у секундах), s(t) –
положення тіла на прямій
(координата даної матеріальної
точки, що рухається у момент
часу t по відношенню до початку
відліку (у метрах).
Знайти швидкість руху тіла в момент часу t.
Розв`язання
Нехай тіло в момент часу t було в точці А і пройшло шлях ОА= s(t).
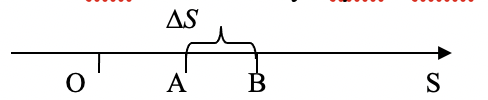
Надамо аргументу t приріст Δt і розглянемо ситуацію в момент часу t+Δt. Координата матеріальної точки змінилась, бо тіло пройшовши шлях від початку руху ОВ= s(t+Δt), перебуватиме в точці В.
Отже, до Δt секунд тіло перемістилося з точки А в точку В, тобто пройшло шлях АВ.
АВ=ОВ-ОА= s(t+Δt)-s(t).
Візьмемо відрізок АВ= ΔS (м)
Шлях ΔS(м) тіло пройшло за Δt секунд.
Нескладно знайти середню швидкість руху Vс за проміжок часу:
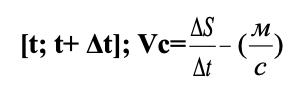
Що означає V(t) в момент часу t (інколи її називають миттєвою швидкістю)?
Можна сказати так : це середня швидкість руху за проміжок часу [t; t+Δt] за умовами, що Δt витрачається все менше і менше; інакше за умови, що Δt О. Це означає, що:
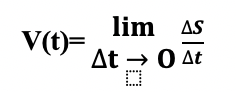
ΔS називається приростом шляху.
Похідною функції f(x) у точці х0 називається границя (якщо вона існує) відношення приросту функції у точці х0 до приросту аргументу Δх, якщо приріст аргументу прямує до нуля і позначається f'(x0).
Дія знаходження похідної функції називається диференціюванням.

- Похідна функції має такий
фізичний зміст: похідна
функції в заданій точці –
швидкість зміни функції
в заданій точці. - Похідна функції має такий
геометричний зміст: похідна
функції в заданій точці є
кутовим коефіцієнтом дотичної
до графіка функції в цій точці,
тобто дорівнює
тангенсу кута нахилу дотичної до графіка функції в заданій точці.
Запам’ятайте!

Можна визначити похідні вищих порядків. Похідною n-го порядку (n-ною похідною) називається похідна від похідної (п – 1) порядку.
Алгоритм знаходження похідної функції у= f(х)
1. Зафіксувати значення х0, знайти f(х0)
2. Надати аргументу х0 приріст ∆х, перейти в нову точку х0+∆х, знайти f(х0+∆х)
3. Знайти приріст функції: ∆у= f(х0+∆х)- f(х0)
4. Скласти відношення:

5. Обчислити границю:
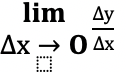

Леонард Ейлер перший почав
використовувати позначення ∆
(дельта) грецька буква для
позначення приросту аргументу
∆х=х1-х0 або х0 і х1 = х0+ ∆х.
Різниця х1- х0= ∆х називається
приростом аргументу.
Приріст функції ∆у=у1-у0 або
різниця f(х1)-f(х0)= f(х0+∆х)- f(х).
Відкриттю похідної і основ
диференціального числення
передували роботи математика
і юриста П`єра Ферма (1601-1665),
який у 1929 р. запропонував
проведення дотичних до довільних
кривих, що фактично спиралися на застосування похідних.
Ісаак Ньютон прийшов до поняття похідної, розв`язуючи задачі про миттєву швидкість.
Готфрід Лейбніц дійшов до похідної функції розглядаючи геометричну задачу про проведення дотичної до кривої.
Для кращого засвоєння нового матеріалу, переглянь, будь ласка, наступне відео:
Давайте перевіримо як ви засвоїли матеріал!
Домашнє завдання: Дано графік функції у=f(х). на ньому вибрана точка А(х0; f(х0)), через яку до графіка проведено дотичну (вважаємо, що дотична існує). Знайти кутовий коефіцієнт дотичної.



