Ми всі чи не щоденно проводимо різні спостереження, досліди, експерименти або випробування. І часто їх результати просто неможливо передбачити заздалегідь.

Наприклад, ми купили лотерейний квиток і не знаємо напевно – виграшний він чи ні. (або зробимо вигляд, що не знаємо 🙂 Але ми можемо оцінити шанс появи бажаного результату. В цьому нам допоможе теорія ймовірностей.
Теорія ймовірностей – математична наука, що вивчає закономірності в явищах і дослідах, результати яких не можна заздалегідь передбачити.
Вважають, що зародження теорії ймовірностей почалося з двох питань відомому французькому математику (і не тільки) Блезу Паскалю.
- Скільки раз потрібно підкинути гральні кості, щоб випадків випадання одночасно двох шісток було більше половини від загальної кількості підкидів?
- Як справедливо розділити гроші, поставлені на кін, якщо гравці припинили гру передчасно?
Друге питання лишимо поки що поза нашою увагою, а ось на перше спробуємо разом знайти відповідь 🙂
Що ще стало поштовхом для розвитку теорії ймовірностей?
Виникнення страхової справи, а саме з кінця XVII століття на науковій основі стало проводитися страхування від нещасних випадків і стихійних лих.
Поміркуй, навіщо страховим компаніям використовувати теорію ймовірностей.

У XVI-XVII століттях у всіх країнах Західної Європи поширилося страхування судів і страхування від пожежі. У XVIII столітті були створені численні страхові компанії та лотереї в Італії, Фландрії, Нідерландах.
Потім методи теорії ймовірностей стали широко застосовувати в демографії, наприклад при веденні статистики народження і смерті.
Події, їх види і що їх пов’язує з теорією ймовірностей
Подія – це основне поняття в теорії ймовірностей. Явище, про яке можна сказати, що воно відбувається або не відбувається за певних умов. Події позначаються великими літерами латинського алфавіту: А, В, С,…
Будь-яка подія відбувається внаслідок випробування (експерименту, досліду).
Випробування – це умови, за яких відбувається (чи не відбувається) подія.
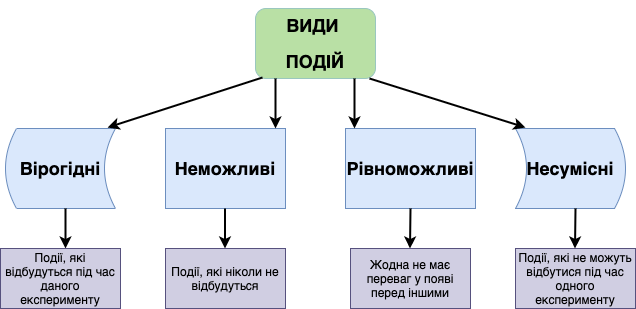
Розглянемо декілька прикладів, щоб зрозуміти в чому різниця між цими подіями з практичної точки зору.
- Вірогідні. Після неділі настане понеділок. Твердження, яке не піддається сумнівам.
- Неможливі. Периметр ромба зі стороною 3 см дорівнює 100 см.
- Рівноможливі. Підкидаючи гральні губики, може випасти як 2, так і 5 з однаковою ймовірністю.
- Несумісні. Подія А – на монеті випадає герб. Подія Б – на монеті випадає решка. Подія А та Б вважаються несумісними.
Мерщій до практики
Спробуємо застосувати теорію ймовірності на практиці.
P(A) – ймовірність події. Її можна обчислити за формулою 1.1.
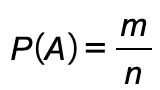
де, m – кількість способів, якими може з’явитися дана подія під час одного експерименту;
n – загальна кількість подій під час даного експерименту (множина елементарних подій).
Поміркуйте, чи може одна з рівноможливих подій мати перевагу над іншою? (відповідь наприкінці цієї глави)

Приклад 1. Поклавши одне морозиво до порожньої морозильної камери, за годину дістанете дві пачки;
Приклад 2. Підкинувши гральний кубик – випаде сімка.

Приклад 1. Ймовірність що після літа настане осінь (100%);
Приклад 2. Підкидаючи гральний кубик випаде число менше ніж сімка (100%).

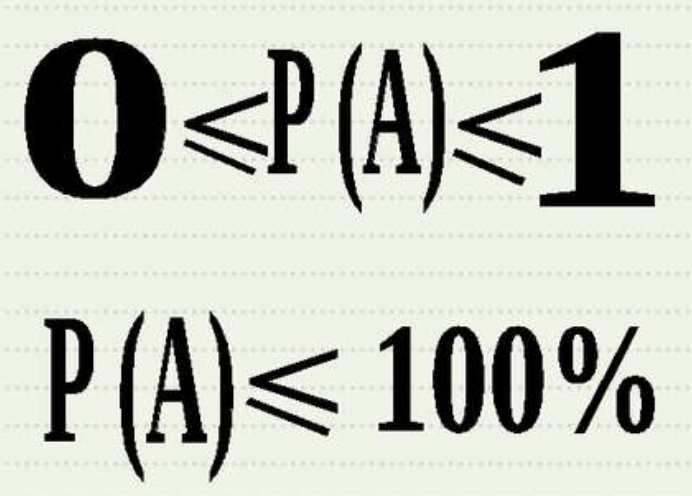
З рис. 1 видно, що ймовірність події може бути більшою або рівнятися 0 і бути меншою або дорівнювати 1 .

Відповідь на запитання. Ті хто відповів ні – безперечно праві. Але в усіх правилах є виключення. Наприклад, якщо у монети або кубика зміщений центр ваги, то набагато частіше будуть випадати цілком певні межі 🙂 В цьому випадку передбачити значення на кубику легше. Але, зазвичай ми вважатимемо що усі наші кубики і монети з прикладів не мають браку.
Перші самостійні кроки по теорії ймовірності
ЗАДАЧА № 1
Знайти ймовірность того, що на гральному кубику випаде більше трьох очок при його підкиданні.
Роз’яснення розв’язку

Дана подія А – під час цього експерименту, більше трьох очок може з’явитися у трьох випадках. Якщо випаде 4, 5 або 6. Отже, m=3, всього граней у звичного кубика 6, значить і загальна кількість подій – n=6.
Р(А)=m/n=3/6=1/2=50%
Відповідь: ймовірність того, що значення на гральному кубику буде більше, чим 3, складає 50% або 1/2.
Перевіримо, чи вдалося тобі засвоїти базову формулу теорії ймовірності.
Пояснення до розв’язання тестових завдань
Дуже тішимось, якщо усі твої відповіді були вірними – ми тоді на правильному шляху. Мерщій перемикай на наступний розділ 🙂
Якщо десь було допущено помилку, не засмучуйся, розглянемо з тобою кожен тест окремо.
- Шістка на гральному кубику одна (m=1), як і будь яка інша цифра. Загальна кількість цифр шість (n=6). Р(А)=m/n=1/6;
- Підкинь но монетку 🙂 Там всього дві грані, і якщо у тебе “чесна” монетка, ймовірність того, що випаде герб або решка рівноможлива і складає 50%. Р(А)=m/n=1/2;
- Підкинь но монетку 🙂 Там всього дві грані, і якщо у тебе “чесна” монетка, ймовірність того, що випаде герб або решка рівноможлива і складає 50%. Р(А)=m/n=1/2;
Завдання для самоперевірки
Завдання 1
Завдання 2, 3, 4
ЗАВДАННЯ №5 ускладнимо 😉

В коробці знаходиться 5 жовтих кульок та 7 блакитних.
Яка ймовірність того, що витягнувши кульку, вона буде жовтого кольору?

Сподіваємось, знайомство з теорієї ймовірностей тебе не дуже налякало і наступного разу ми зможемо перейти до розв’язання більш складних прикладів і нарешті спрогнозувати ймовірність виграшу у лотерею 🙂



