
У житті часто доводиться що-небудь обирати з великої кількості всіляких варіантів. Наприклад,
• скількома способами можна розташовувати в турнірній таблиці 10 футбольних команд, якщо жодні дві з них не набрали порівну очок?
• скількома способами можна скласти розклад на день із 4 навчальних предметів для однієї групи, якщо в групі вивчається 9 предметів?
• cкільки п’ятицифрових чисел можна скласти із цифр 1,2,3,4,5, якщо цифри в числі не повторюються?
Відповідаючи на ці запитання, потрібно підрахувати, скільки різних комбінацій, утворених за певним правилом, можна скласти з елементів заданої скінченної множини. Для таких задач існують загальні методи розв’язування, що вивчає комбінаторика як розділ математики.
Елементи комбінаторіки
Згадайте, що з деякими елементами комбінаторики ви вже ознайомилися в попередніх класах.
Скінченна упорядкована множина – така множина, для якої визначений порядок розміщення її елементів.

Комбінаторика – розділ математики, у якому
вивчають способи вибору та розташування
елементів з деякої скінченної множини, які
відповідають певним умовам.
Ці правила визначають спосіб побудови
деякої конструкції – комбінаторної сполуки.
Основа класичної комбінаторики – комбінаторні
правила суми та добутку.
Наприклад (правило суми). На тарілці лежать 5 яблук і 9 груш. Один плід можна обрати 5+9=14 способами.
З цієї задачі маємо правило суми:

Якщо деякий елемент А можна вибрати т способами,
а елемент В — r способами (причому будь-який вибір
елемента А відрізняється від вибору елемента В), то
вибрати А або В можна т + r способами.
Розглянемо другий приклад . На пошті в продажу є 5 різних конвертів і 3 різні марки. Скількома способами можна купити конверт з маркою?
Розв’язання. 1-й спосіб.
Намалюємо дерево можливих
варіантів (мал.1). Позначимо
конверт буквою К, марку – буквою М.
Малюємо від стовбура 5 гілок (оскільки є 5 видів конвертів). Оскільки маємо 3 марки, то від кожної з п’яти отриманих точок
Малюємо по 3 гілки. Рахуємо кількість отриманих внизу точок – 15 і отримуємо відповідь до задачі. Дерево можливих варіантів, до речі, дає змогу розв’язувати різноманітні задачі, пов’язані з обчисленням кількості способів.
2-й спосіб. Оберемо конверт. У комплект до нього можна вибрати будь-яку з трьох марок. Тому є 3 комплекти, що містять обраний конверт. Оскільки конвертів усього 5, то кількість різних способів становить 15 (5 ∙ 3 = 15).
Дійшли до важливого правила комбінаторики – правила добутку:

Якщо елемент А можна обрати m способами, а після
кожного такого вибору інший елемент В можна
обрати (незалежно від вибору елемента А) n способами,
то пару елементів А і В можна обрати m ∙ n способами.
Правило добутку можна використовувати, якщо треба обрати більше 2 елементів.
Приклад 3. На пошті в продажу є 5 різних конвертів, 3 різні марки і 4 різних вітальні листівки. Скількома способами можна купити комплект, що містить конверт, марку та листівку?
Розв’язання. 5 ∙ 3 ∙ 4 = 60 способів.
Розглянемо далі задачу, у якій треба полічити кількість способів, якими можна розмістити в ряд певну кількість предметів.
Факторіал та перестановки.
Перш, ніж ми перейдемо до вивчення наступних понятть, давайте розглянемо дуже важливе поняття комбінаторіки. Це факторіал.

Факторіалом числа n, де n— ціле невід’ємне число, називають добуток усіх натуральних чисел від 1 до n. Позначають це так: n! (читають: «ен факторіал»). Отже, n! = 1 • 2 • 3 • … • (n — 1) • n.
За означенням приймають 0! = 1.
Наприклад, 4! = 1 • 2 • 3 • 4 = 24.
Розглянемо приклад.
Зоя, Оля та Ян зайшли до шкільного буфету. Скількома способами вони можуть вишикуватися в чергу?
Зрозуміло, що існує 6 варіантів.
Зоя, Оля, Ян Оля, Ян, Зоя Ян, Зоя, Оля Зоя, Ян, Оля Оля, Зоя, Ян Ян, Оля, Зоя
Ще один приклад. Денний розклад містить 7 уроків. Скількома способами можна скласти денний розклад так, щоб усі 7 уроків були різними? Іншими словами, скільки існує перестановок із 7 уроків? Подібні задачі називають задачами на знаходження кількості перестановок. Кількість перестановок із n елементів позначають символом Pn (читають: «пе з ен»; Р – перша літера від франц. слова permutation – перестановка).
Для будь-якого натурального n справедлива формула:
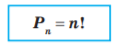
Отже, троє дітей можуть вишикуватися в чергу 3! = 6 способами, а кількість розкладів із 7 уроків дорівнює 7! = 5040.
Задача 1. Скількома способами 5 машин можуть вишикуватися в колону? Р оз в’яз анн я. У даній задачі треба обчислити кількість перестановок із 5 елементів. Використовуючи формулу (1), маємо: P5 = 5! = 120. В і дп о в і д ь: 120.
Задача 2. Дитина грається трьома іграшками: машиною, трактором, кораблем. Скількома способами їх можна викласти в ряд?
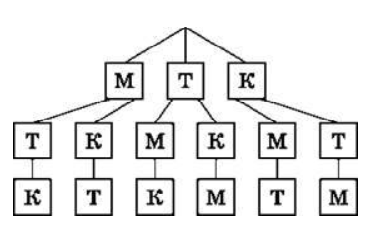
Розв’язання. На перше місце
можемо поставити одну з трьох
іграшок: машину, трактор або
корабель. Після цього на друге
місце можна поставити одну з
двох наступних іграшок. Після
цього на третє місце ставимо
одну іграшку, яка залишилася
після вибору перших двох.
Використовуючи правило добутку, знайдемо, що іграшки можна розмістити
шістьма різними способами (3 ∙ 2 ∙ 1). Перевіримо розв’язок задачі за допомогою
дерева можливих варіантів (мал.1).
Обчислити кількість способів, якими можна розмістити в ряд кілька предметів – перестановки, ми можемо за допомогою поняття факторіал. У нашій задачі кількість перестановок з трьох елементів дорівнює: Р3 = 1 ∙ 2 ∙ 3; аналогічно кількість перестановок з двох елементів Р2 = 1 ∙ 2; із чотирьох елементів Р4 = = 1 ∙ 2 ∙ 3 ∙ 4 = 24; з п’яти Р5 = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 = 120 і т. д.
І як завжди, закріпити вивченний матеріал ми пропонуюємо вам відео-контентом, з якого ви дізнаєтесь базисні поняття комбінаторіки, а саме факторіал – що це таке і як його рахувати. Також, розглянемо як рахувати кількість перестановок з деякого числа елементів. При чому це буде зроблено на конкретному, простому прикладі, після чого, ви зможете використовувати ці знання і у більш складних випадках.
Дивимось!
Домашнє завдання.
1.Підручник стор. 125 – 130 (на стор. 130 читати тільки тему “Перестановки”)
2. Виконати завдання: 14.5; 14.7 (стор.133).



